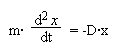
Schwingungen
1. Harmonische Schwingung (Elastische, ungedämpfte Schwingung)
Wirkt auf ein Teilchen nur eine elastische, d.h. zur Auslenkung proportionale und ihr entgegengesetzte Rückstellkraft (F = -D·x), vollführt das Teilchen eine sinusförmige Schwingung:
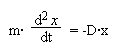
Die Lösung der Gleichung ist
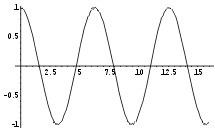
x(t) = c1·cos(w·t) + c2·sin(w·t) bzw.
x(t) = A·cos(w·t + j), wobei ![]()
2. Gedämpfte Schwingung:
Wenn außerdem noch eine Reibungskraft (F = -R·v) wirkt, die der Teilchengeschwindigkeit entgegengerichtet ist, ist die Schwingung gedämpft.
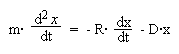
Die Lösung der Gleichung ist
![]()
Je nachdem, ob der Ausdruck unter der Wurzel größer, kleiner oder gleich Null ist, ergeben sich folgende Lösungen:
a. Kriechfall: ![]()

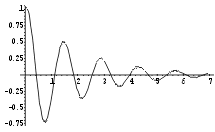
b. Schwingfall: ![]()
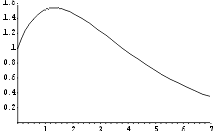
c. Aperiodischer Grenzfall: ![]()
Beispieltabellen:
federpendel.xls
schwingung.xls
Erweiterungen und Ausblicke:
Masseteilchen an Spiralfeder taucht in Flüssigkeit ein ->
Stokes-Reibung:
F = -6p h r v
- Stokes-Reibung: proportional zur Geschwindigkeit -> Amplitude
nimmt mit e-Funktion ab
- Coulomb-Reibung: unabhängig von der Geschwindigkeit -> Amplitude nimmt linear ab
- Newton-Reibung: proportional zum Quadrat der Geschwindigkeit -> Amplitude nimmt
hyperbolisch ab
- Schmiermittel-Reibung: proportional zur Wurzel aus der Geschwindigkeit -> Amplitude
nimmt parabolisch ab
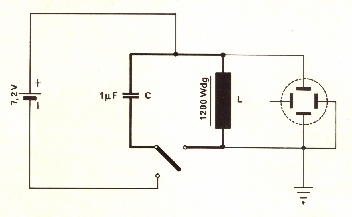
| Mechanischer Schwingkreis | Elektromagnetischer Schwingkreis |
| ungedämpft: | |
|---|---|
x(t) = A·cos(w·t) |
U(t) = U0·cos(w·t) I(t) = I0·sin(w·t) (Strom durch Spule um 90° phasenverschoben!) |
| gedämpft: | |
| m: Masse des Teilchens R: Reibungskonstante D: Rückstellkonstante der Feder 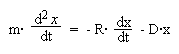 |
L: Induktivität der Spule R: Ohm'scher Widerstand C: Kapazität des Kondensators 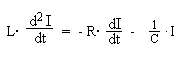 |